Le Compteur Geiger

Partie 1: Compteur Geiger

But de la manipulation:

Introduction à la notion de désintégration aléatoire, notion clé en mécanique quantique, et description statistique des processus aléatoires. Petite introduction à l'analyse de données avec Excel ou Python.

Materiel:

• Montage avec un tube Geiger avec divers points de mesure.
• Oscilloscope digital
• Source radioactive de faible activité.

Précautions:

Il faut manipuler le tube Geiger avec précaution.

Ne jamais démonter le cadre qui entoure la source radioctive, ne pas la manipuler sans nécessité, et rester, sauf pour des manipulations brèves, aussi loin que possible.

Description du fonctionnement:

Le tube Geiger est une chambre métallique cylindrique dans l’axe de laquelle est tendu un mince fil métallique, muni d'une cathode (-) et d'une anode (+) et rempli d’un gaz sous faible pression.

Le tube est maintenu avec une tension élevée sans provoquer l'ionisation spontanée du gaz. Lors du passage d'un rayonnement ($\alpha$, $\beta$, ou $\gamma$), des électrons peuvent être arrachés en ionisant les atomes de gaz.

Schématisation d'un compteur geiger. (Source: By Marken64 via Wikipedia Commons)

L'intensité du signal dépend de la tension appliquée au tube et nous pouvons distinguer trois modes de fonctionnements/regions:

• Chambre d'ionisation: Pour de faibles tensions, les électrons et ions se dirigent vers les électrodes. Le courrant induit est independent de l'energie du rayonnement.

Visualitation du mode d'operation de la chambre d'ionisation. (Source: by Doug Sim via Wikimedia Commons)

• Mode proportionnel: Pour cette région de tensions, les électrons entraînent la libération de nouvelles charges secondaires (avalenches). Le signal récolté est proportionnel aux charges déposées dans le tube par le rayonnement initial.

Visualitation du mode d'operation de la chambre proportionnel. (Source: by Doug Sim via Wikimedia Commons)

• Mode Geiger: Les electrons provoquent des intéractions secondaires, voire tertiaires et il y a une saturation. Le signal observé est indépendant de l'ampleur de l'ionisation initiale. Il se peuvent creer aussi de photons UV qui peuvent initié des autres avalanches.

Visualitation du mode d'operation de la chambre proportionnel. (Source: by Doug Sim via Wikimedia Commons)

Regions de fonctionnement d'un compteur geiger. (Source: by Doug Sim via Wikimedia Commons)

Manipulation

Nous allons utiliser un compteur geiger avec une circuit home-made qui nous permettra determiné le debut de la region geiger. L'appareillage peut-être representé avec le montage suivant.

Typical operating circuit.

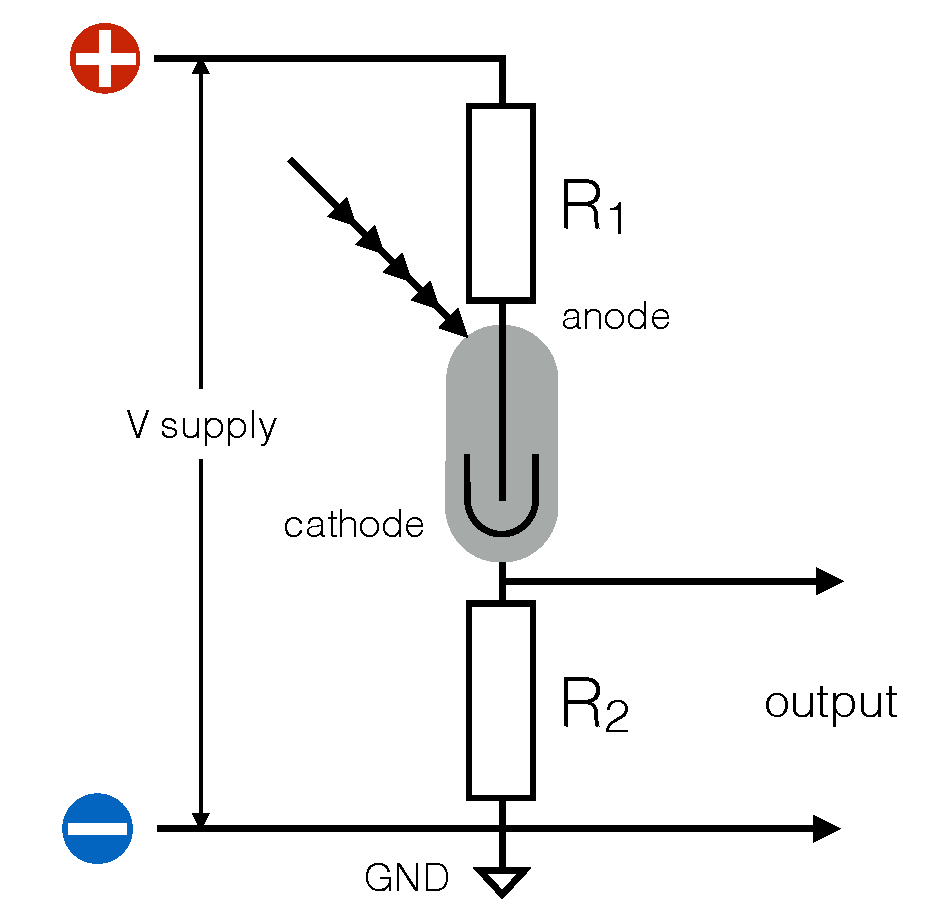
L'ionisation du tube est observée par le courant qui en résulte, et qui est mesuré par la tension aux bornes de la résistance de cathode (R2). Dans notre montage, le valeurs des résistances R1 et R2 sont 10 M$\Omega$ et 220 K$\Omega$. La haute tension recommandée pour le tube utilisée est de 500 V.

La tension maximale à ne pas dépasser est de 600 V (le circuit devrait empècher que l'on dépasse cette tension maximale)

Même si 500 V n'est pas considéré en électricité comme de la Haut Voltage, c'est plus dangereux que les 220 V distribué dans les prises. Soyez toujours prudent en manipulant des tensions élevées.

Pour récolter les signaux, nous allons nous aider de l'oscilloscope. Une sonde X10 permet d'avoir une impédance d'entrée de 10 M$\Omega$ afin d'éviter de charger exessivement le circuit du Geiger.

Procédure pour la détermination de la region Geiger

Nous allons rechercher la tension nécessaire pour que le signal de sortie deviene indépendant de la tension appliquée au circuit

1. Faire varier la valeur de la haute tension pour déterminer la plage Geiger.
2. Choisir une valeur permettant un déclenchement fiable.
3. Dessiner la trace obtenue
4. Expliquer son origine.

Question: Compte-tenu de votre observation, quelle est la période après déclenchement pendant laquelle la tension au bord du tube tombe en-dessous de la valeur Geiger? (cette valeur sera à mettre en relation avec le temps mort ci-dessous).

Procédure pour la détermination du temps mort

Après un déclenchement, le tube Geiger ne réponds plus pour une petite période après la décharge. C'est le bien nommé temps mort du tube Geiger.

Temps mort d'un tube Geiger. (Source: By Dougsim via Wikimedia Commons)

Pour vérifier ce phénomène, nous gardons le dispositif précédent en prenant une base de temps avec l'oscilloscope suffisamment longue pour pouvoir observer une seconde, une troisième ou plusieurs décharges après la première.

L'oscilloscope reste avec le déclenchement normal. Quand une première décharge a lieu il va fournir une trace. Cette trace pourra alors comporter une deuxième/troisième/etc. décharge. Si nous observons pour un temps suffisamment long nous allons observer qu'aucune décharge n'est observée dans un intervalle de temps après le déclenchement: c'est le temps mort.

Utiliser une rémanence infinie, en mode déclenché, accumuler les traces. On voit une image similaire à la Figure 7. En déterminer la valeur du temps mort.

Partie 2: Désintégrations aléatoires

But de la manipulation:

Le but de cette manipulation est d'étudier le caractère aléatoire des désintégrations nucléaires, en rapport avec la mécanique quantique.

Introduction

Radioactivité

La radioactivité d'un matériau est due aux transitions d'une nucléon instable vers une structure plus stable. La différence d'énergie entre l'état initial et l'état final peut être libéré de différentes façon :

• Ejection d'une particule $\alpha$, c'est à dire un noyau d'hélium (2 protons + 2 neutrons)
• Ejection d'un neutron
• Ejection d'un photon de haute énergie ou rayonnement-$\gamma$. Dans ce cas, non seulement les forces nucléaires sont impliquées, mais également la force électromagnétique
• Ejection d'un électron (appelé une particule $\beta$) ou d'un positron ($\beta^+$). Dans ce cas, un neutrino $\nu$ et un antineutrino $\bar{\nu}$ seront également émis. Cette réaction se passe uniquement pour le neutron quand il est isolé (i.e. jamais pour un $p$ isolé) puisque la masse du neutron est plus haute que les produits :

$$ n \rightarrow p + e^- + \bar{\nu}$$

A l'intérieur d'un nucléon, cependant, l'énergie de liaison peut donner de l'énergie, donc le processus suivant est autorisé :

$$ N^Z \rightarrow N^{Z - 1} + e^+ + \nu$$

L'énergie libérée dans cette radioactivité peut varier significativement (du keV au MeV) et est plus grande que les réactions chimiques typiques (normalement sous 1 eV).

Distributions de probabilité

C'est au delà du cadre de ces notes de donner une introduction rigoureuse aux statistiques et probabilités. Cependant nous pouvons revoir quelques notions basiques, comme la variable, la variable aléatoire et la distribution de densité de probabilité.

• Une variable peut être n'importe quelle quantité, propriété qui peut prendre différentes valeurs d'un set spécifié.
• Quand une variable est le résultat d'un processus aléaloire ou d'une expérience, nous appelons cette variable une variable aléatoire.
• Une fonction de densité de probabilité (pdf pour "probability density function") nous donne la probabilité qu'une variable aléatoire donnée prenne une valeur particulière.

Quand une variable aléatoire peut prendre seulement des valeurs discrètes (par exemple 0, 1, 2, 3,...) la fonction de densité de probabilité est appelée une distribution discrète de probabilité ou fonction de masse (pmf pour probability mass function)

Exemple:

Imaginez une source radioactive qui produit une moyenne de 1.5 désintégration par seconde (ie, 1.5 Bq). Si nous mesurons pendant une longue période, 1 minute, nous allons observer à peu près 90 désintégrations ce qui donne 90/60 = 1.5 Bq. Cependant si nous mesurons durant une petite période de temps, 1 s, nous n'allons pas observer exactement 1.5 désintégration, mais seulement des valeurs discrètes.

Dans l'exemple ci dessus, on peut prouver que les désintégrations d'un nucléon suivent la distribution discrète de poisson:

$$\mathcal{P}(n|\mu) = \frac{\mu^n e^{-\mu}}{n!}$$

Où $n$ est la variable aléatoire (dans notre cas le nombre de désintégrations) qui ne peut prendre que des valeurs discrètes $n = 0,1,2,3,...$ et $\mu$ et la valeur moyenne, 1.5 dans l'exemple ci-dessus.

La distribution de Poisson nous dit la probabilité de mesurer en une seconde un nombre donné de désintégrations quand la moyenne est $\mu = 1.5$.

La suite est un petit exemple en python pour faire l'histogramme de la distribution de poisson. Ces distibutions sont utilisées vraiment souvent et c'est pourquoi certains outils d'analyse comme scipy ont déjà implémenté cette fonction.

Également, sous les tableurs OpenOffice Calc ou Excels, le distribution de Poisson et Gaussienne sont données par les fonctions POISSON(x;mu;FALSE) et NORMDIST(x;mu;sigma;FALSE) ou POISSON.DIST(x;mu;FALSE) et NORM.DIST(x;mu;sigma;FALSE) dans les nouvelles versions d'Excel (voir Statistical functions in Excel).

#For inline plotting
%matplotlib inline
import matplotlib.pyplot as plt

#Seaborn for nicer plots. Seaborn is not a python default package. Comment out these lines if seaborn is not installed
import seaborn as sea
sea.set_style("dark")
sea.set_context("poster")

#import the statistics tools from scipy and numpy
from scipy.stats import poisson
import numpy as np

#we create a poisson distribution with mean = 1.5
P = poisson(1.5)

#List of values where we want to test the distribution
n = np.array([0,1,2,3,4,5,6,7])

ax = plt.subplot(111)

#We plot the probability mass function (pmf) for the list of values n
ax.plot(n, P.pmf(n),'o', ms=10, color="green")

#labels and showing 
ax.set_ylabel("$\mathcal{P}(n|\mu = 1.5)$")
ax.set_xlabel("n")
plt.grid()
plt.show()

Une autre distribution importante est la distribution gaussienne. C'est la distribution typique des incertitudes dans une mesure, par exemple lorsque nous voulons mesurer la distance entre deux points et que nous répétons la mesure plusieurs fois, la distribution suivra une gaussienne. La distribition dépend de deux paramètres: la moyenne $\mu$ et la variance $\sigma^2$.

$$\mathcal{N}(x|\mu, \sigma^2) = \frac{1}{\sigma \sqrt{2\pi}} \exp\left(\frac{-(x-\mu)^2}{2\sigma^2}\right)$$

La distribution gaussienne est un exemple de distribution continue.

from scipy.stats import norm
#Normal or Gaussian distribution with mean = 1.5 and sigma = 1.5
G = norm(1.5,1.5)

#List of continues values we want to test the gaussian distribution. 100 values from 0 to 7
n = np.linspace(0,7,100)

ax = plt.subplot(111)

#We plot the probability density function (pdf) on every point.
ax.plot(n, G.pdf(n),'-', lw=3, color="green")

#labels
ax.set_ylabel("$\mathcal{N}(x|\mu = 1.5, \sigma = 1.5)$")
ax.set_xlabel("x")
plt.grid()
plt.show()

Propriétés des distributions de probabilité.

• Normalisation: Comme toutes les distributions de densité de probabilité, les distributions de Poisson et Gaussienne sont normalisées (ie la somme de toutes les probabilités doit être 1.)

$$\sum_{n=0}^{\infty}\mathcal{P}(n|\mu) = 1$$$$\int_{-\infty}^{\infty} \mathcal{N}(x|\mu, \sigma^2) = 1$$

• Moyenne: Le premier moment ou moyenne peut être calculé comme:

$$\sum_{n=0}^{\infty} n \cdot \mathcal{P}(n|\mu) = \mu $$$$\int_{-\infty}^{\infty} x \cdot \mathcal{N}(x|\mu, \sigma^2) = \mu$$

• Variance: Le second moment ou variance $\sigma^2$ est donnée par:

$$\sigma^2 = \sum_{n=0}^{\infty} (n-\mu)^2 \cdot \mathcal{P}(n|\mu) = \mu $$$$\sigma^2 = \int_{-\infty}^{\infty} (x - \mu)^2 \cdot \mathcal{N}(x|\mu, \sigma^2) $$

Notez que pour la distribution de Poisson, la variance et la moyenne sont liés.

Procédure

Pour cette partie de l'expérience, nous allons utiliser un compteur geiger commercial venant de GAMMA-SCOUT. Vous pouvez visiter leur page pour vous familiariser avec l'appareil. En particulier les étudiants sont invités à lire le manual .

Bruit de fond

On va mesurer le niveau de radiation ambiante. Pour ça on va utiliser deux techniques pour la mesure.

• Mesure sur un temps long: on sélectionne un temps de mesure de l'ordre de la minute ou de quelques minutes. Effectuer trois mesures.
• Mesure répétée sur un temps court: Le but ici est d'illustrer le caractère aléatoire de ce bruit. On mesurera au moins 100 périodes de 1 seconde.

Traitement de données

Dans le cas de mesure sur un temps court, on va voir comment analyser ces données avec python. On peut également utiliser un tableur informatique comme Excel (Windows, Mac OS), Numbers (Mac OS) ou Apache Open Office Calc (Linux, Windows, Mac OS)

Ci-dessous, une liste de 100 mesures faites en une seconde, où différentes valeurs de désintégration sont mesurées.

data = [0,1,1,0,0,1,2,1,0,1,0,0,1,0,1,0,1,1,1,0,0,2,2,0,1,0,1,0,0,1,2,1,0,2,1,0,0,2,2,0,1,0,1,0,
        1,0,1,0,0,0,1,0,2,0,0,0,0,1,0,4,0,0,0,0,0,1,0,2,1,3,1,1,0,0,0,2,0,0,1,1,0,1,0,3,1,0,0,0,
        1,0,1,0,0,0,0,0,1,0,0,2]
print len(data)

100

Nous pouvons compter nous même la fréquence de chaque mesure, c'est à dire combien de 0 nous avons mesurés, combien de 1,... Mais nous pouvons faire cela directement avec un histogramme.

#Create the axis
fig, ax = plt.subplots()


#Use matplotlib to plot the data in a histogram with 10 bins between 0 and 10
ax.hist(data, bins=10, range=[0,10])
ax.set_xlim(0,5)
ax.set_ylim(0,70)
ax.set_ylabel("Frecuency")
ax.set_xlabel("n")
plt.grid()
plt.show()

Nous pouvons voir que ces mesures suivent une distribution de probabilité où la valeur la plus probable est 0.

Exercice: Divisez votre échantillon de données en deux échantillons de 50 mesures et tracez l'histogramme de fréquence. Suivent ils la même distribution ?

Si nous assumons que les mesures suivent une densité de distribution donnée avec une moyenne $\mu$ et une variance $\sigma^2$ nous pouvons utiliser les formules suivantes pour estimer ces valeurs :

$$\hat{\mu} = \frac{1}{N}\sum_{i=1}^{N}x_i$$$$\hat{\sigma}^2 = \frac{1}{N-1} \sum_{i=1}^{N}(x_i - \hat{\mu})^2$$

Pour l'exemple ci-dessus nous avons :

$$\hat{\mu} = 0.64$$$$\hat{\sigma}^2 = 0.69 \sim \hat{\mu}$$

Donc nous pouvons approximer la distribution par une distribution de poisson avec un $\mu =0.61$

mu =np.sum(data)*1.0/len(data)
sigma = 1/(len(data) -1.0) * np.sum((data - mu)**2)
print mu, sigma

0.64 0.697373737374

#Create the axis
fig, ax = plt.subplots()

#Use matplotlib to plot the data in a histogram with 10 bins between 0 and 10
ax.hist(data, bins=10, range=[0,10], label="Data")
ax.set_xlim(0,5)
ax.set_ylim(0,70)
ax.set_ylabel("Frecuency")
ax.set_xlabel("n")

P = poisson(0.64)
G = norm(0.64, np.sqrt(0.697))

counts = np.array([0,1,2,3,4])
ax.plot(counts, len(data)*P.pmf(counts),'o', ms=20, color="green", label="$\mathcal{P}(n|\mu = 0.64)$")

x = np.linspace(0, 5, 100)
ax.plot(x, len(data)*G.pdf(x),'-', lw=3, color="red", label="$\mathcal{N}(x|\mu = 0.64, \sigma^2 = 0.697)$")


plt.legend(loc="upper right")
plt.grid()
plt.show()

Notez que nous avons multiplié les probabilités par le nombre de mesures (100) pour faire correspondre la distribution de densité et l'histogramme de fréquence. Nous pouvons voir que la distribution de Poisson est une bonne description de ce processus aléatoire.

Question: Y a t'il une cohérence entre vos mesures pour des temps longs et des temps courts?

Il est intéressant de savoir combien l'estimation de la moyenne peut s'écarter de la valeur idéale correspondant à une infinité de mesures dans un dispositif constant. Statistiquement, cet écart est donné par:

$$\sigma_\mu = \frac{\sigma}{\sqrt{N}}$$

Où on peut voir que l'écart va diminuer avec un nombre considérable de mesures. Pour la moyenne, nous avons

$$\hat{\mu} \pm \sigma_\mu$$

Cette erreur est l'erreur statistique. Il y a aussi des erreurs systematiques (précision de l'appareil, efficacité du compteur, etc..). Ces erreurs sont traitée indépendamment, et il convient alors d'ajouter séparément:

$$\hat{\mu} \pm \sigma_\mu \pm \sigma_{syst.}$$

Mesures d'une source radioactive

Vous disposez d'une source radioactive de très faible intensité. Son effet est presque impossible à discerner du bruit de fond quand le compteur est à quelques décimètres de la source.

Il est toutefois essentiel de vous conformer aux instructions précises des enseignants pour la manipulation de cette source

Intensité du rayonnement en fonction de la distance.

1. Placez la source à diverses distances du détecteur, par exemple: 1, 2, 5, 10 cm.
2. Dans chaque cas choisissez un temps de comptage qui vous donne une mesure de l'ordre de 100 coups au moins. (vous pouvez choisir le temps correct après un essai éventuel).
3. Calculez le nombre de coups par seconde dans chaque cas, et portez en graphique.

Question: Quelle loi attendez-vous pour le graphique du nombre de coups en fonction de la distance?

Reminder: N'oubliez pas de soustraire la contribution du bruit de fond de chacune de ces mesures.

Testez si le comportement est bien en $1/R^2$ où $R$ est la distance. On peut faire un ajustement de courbes dans un tableur pour le tester. Si une composante des rayonnements est absorbée rapidement par l'air, elle devrait se manisfeter ici comme un excès à petite distance. C'est le cas du rayonnement $\alpha$, mais toutefois, l'atténuation de rayonnement $\alpha$ est trop rapide pour qu'il puisse être mis en évidence.

Intensité de la source

A partir des données ci-dessus, on peut estimer le nombre de rayons ionisants émis par la source par seconde. Il faut compter que le compteur intercepte le rayonnement par une petite fenêtre de l'ordre de 1 cm$^2$.

Il est fortement déconseillé d'essayer de mesurer la fenêtre directement car il s'agit d'une fenêtre de mica particulièrement fragile. Demander la valeur exacte de la surface au laboratoire.

Le rayonnement émis par la source est en principe isotrope, et réparti également sur une sphère dont le diamètre est la distance au détecteur. Un calcul simple donne alors l'intensité de la source en désintégrations par seconde ou Becquerel (Bq). Il faut tenir compte que le détecteur est situé à 1 cm à l'interieur du boîtier pour l'appareil gamma-scout.

Statistique de Poisson pour la source

Nous répétons ici l'exercice fait pour le bruit de fond

1. Placez la source à une distance qui donne un signal de l'ordre de 20 coups/seconde (afin que le bruit de fond soit négligeable).
2. Mesurez le rayonnement pendant N (au moins 100) périodes de 1 s.
3. Traitez comme pour le bruit de fond (histogramme, moyenne, graphique, comparaison aux distributions standards)
4. Séparez les N/2 premières données et les N/2 données et traitez séparément. Présentez dans chaque cas les résultats sous la forme $\hat{\mu} \pm \sigma_\mu$. Ces mesures sont-elles compatibles?

Mesures entachées d'erreurs aléatoires

Nous avons étudié un phénomène physique qui était de nature aléatoire. Toutefois, des techniques similaires peuvent s'appliquer à une autre situation : celle où le phénomène n'est pas aléatoire mais où sa mesure est entachée d'erreurs de type aléatoires.

Example:

Pour déterminer la période d'un pendule avec un simple chronomètre à main, on peut compter globalement une suite d'oscillations pour que l'erreur statistique associée soit négligeable par rapport à la mesure.

Dans l'exemple ci-dessus, la solution pour réduire l'erreur statistique est simple. Compliquons le problème: nous souhaitons mesurer la période en fonction de l'amplitude (le pendule n'est pas isochrone, la période dépend de l'amplitude). Dans ce cas il faut mesurer individuellement la période d'une oscillation. L'erreur sur chaque mesure individuelle est élevée. Si nous répétons cette mesure un grand nombre de fois on obtient une série de mesures, qui résultent de la superposition d'une quantité reproductible et d'une composante fluctuante.

Procedure pour l'étude des erreurs statistiques

1. Choisissez la longueur d'un pendule pour se trouver au voisinage de 1 seconde. On commence pour une amplitude de $45^{\circ}$.

2. Mesurez avec l'aide d'un chronomètre à main la période une fois. Répétez cette mesure au moins 50 fois.

3. Traitez ces séries de mesures comme précédemment: déterminez la moyenne, la variance, portez en histogramme. A quelle distribution s'approxime la distribution de données?

Comme précédemment, on notera que:

$$\hat{\mu} \pm \sigma_\mu \pm \sigma_{syst}$$

On peut réduire $\sigma_\mu$ d'un facteur racine carrée de N. Notons toutefois que il y a aussi un effet systematique (précision du chronomètre, la tendance de l'observateur à anticiper la mesure, etc.)

---

Revision J.A. Aguilar 2015

JM Frère, P. Duhamel, A. Karusho 2012